Polinomio
En matemáticas, se le llama polinomio a la suma de varios monomios. Un monomio es un producto de un coeficiente y una variable elevado a un número natural, que se llama el exponente del monomio.
Ejemplos de monomios son. El siguiente ejemplo describe en detalle las partes de un monomio. Si consideramos el monomio:
es un monomio con coeficiente 6, variable x y exponente 5. Por tanto, el grado de este monomio es 5.
El grado de un monomio es su exponente. El grado de un polinomio es el del monomio de mayor grado. En el polinomio, existe el término independiente, que es un monomio que no tiene parte literal o variable, es decir, que no tiene variables o letras que lo acompañen. Algunos ejemplos:
P(x) = 2, polinomio de grado cero.
P(x) = 3x + 2, polinomio de grado uno.
P(x) = 2x2+ 3x + 2, polinomio de grado dos.
Convencionalmente se define el grado del polinomio nulo como. En particular los números (o elementos del anillo) son polinomios de grado cero.
Definición algebraica
Polinomios de una variable
Para a0, …, an constantes en algún anillo (en particular podemos tomar un cuerpo, como  o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
Las constantes a0,…, an se llaman los coeficientes del polinomio. A a0 se le llama el coeficiente constante (o término independiente) y a an, el coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normado. Siendo x un símbolo llamado indeterminada.
Polinomios de varias variables
Los polinomios de varias variables son similares a los de una variable. La diferencia es que en ellos cada uno de los monomios puede contener más de una letra de variable. Por ejemplo:
Son monomios de varias variables. Más en detalle el último de ellos  es un momonio de tres variables (ya que en él aparecen tres letras x, y y z), el coeficientes es 4, y los exponentes son 1, 2 y 1, ya que xy2z = x1y2z1.
es un momonio de tres variables (ya que en él aparecen tres letras x, y y z), el coeficientes es 4, y los exponentes son 1, 2 y 1, ya que xy2z = x1y2z1.
Operaciones con polinomios
Artículo principal: Operaciones con polinomios
Los polinomios se pueden sumar y restar agrupando los términos y simplificando los monomios semejantes. Para multiplicar polinomios se multiplica cada término de un polinomio por los términos del otro polinomio y se simplifican los monomios semejantes, posteriormente. Por ejemplo:
Para poder realizar eficazmente la operación tienes que adquirir los datos necesarios de mayor a menor. Una fórmula analítica que expresa el producto de dos polinomios es la siguiente:
Clases de polinomios
Polinomio nulo
El polinomio nulo tiene todos sus coeficientes nulos.
Polinomio homogéneo
El polinomio homogéneo tiene todos sus términos o monomios con el mismo grado.
P(x) = 2x2 + 3xy
Polinomio heterogéneo
Los términos de un polinomio heterogéneo son de distinto grado.
P(x) = 2x3 + 3x2 − 3
Polinomio completo
Un polinomio completo tiene todos los términos desde el término independiente hasta el término de mayor grado.
P(x) = 2x3 + 3x2 + 5x − 3
Polinomio ordenado
Un polinomio está ordenado si los monomios que lo forman están escritos de mayor a menor grado.
P(x) = 2x3 + 5x − 3
Polinomios iguales
Dos polinomios son iguales si verifican:
1Los dos polinomios tienen el mismo grado.
2Los coeficientes de los términos del mismo grado son iguales.
P(x) = 2x3 + 5x − 3
Q(x) = 5x − 3 + 2x3
Polinomios semejantes
Dos polinomios son semejantes si verifican que tienen la misma parte literal.
P(x) = 2x3 + 5x − 3
Q(x) = 5x3 − 2x − 7
Tipos de polinomios según el número de términos
Monomio
Es un polinomio que consta de un sólo monomio.
P(x) = 2x2
Binomio
Es un polinomio que consta de dos monomios.
P(x) = 2x2 + 3x
Trinomio
Es un polinomio que consta de tres monomios.
P(x) = 2x2 + 3x + 5
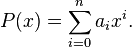
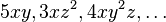



Me encanta*--* Quedo muy bonita :D
ResponderEliminarme duele el cerebro (esta MUY completo)
ResponderEliminar